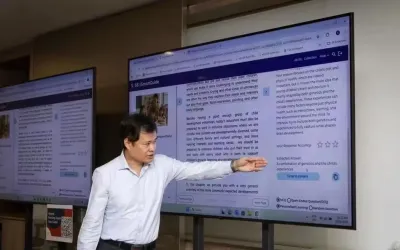
去年的小六會考,一道「海倫和艾凡」(Helen and Ivan)硬幣考題,難倒無數新加坡學生,近幾年,小學離校考試出現刁鑽難解的數學題引起公眾關注和討論,不過教育部強調,小六會考題目的難度多年來都相當一致,比較難的題目最多只占15%。

海倫和伊萬有相同數量的硬幣。海倫有一些5毛錢硬幣和64個2毛錢硬幣。她的硬幣一共1.134千克。伊萬有一些5毛錢硬幣和104個2毛錢硬幣。
問題1:誰有更多的錢,多多少?
問題2:假設每個5毛硬幣比2毛硬幣重2.7克,伊萬的硬幣一共多少千克?
與中國相比,新加坡數學就深明「萬丈高樓從地起」的道理,重視小朋友的數學根基,讓他們了解公式的源頭、概念,填補傳統教學方式的漏洞。
「模型思維」(Model Method)是新加坡數學最重要的特色。成年人可能會覺得代數方法更容易,但年幼的孩童更難理解抽象和機械化的代數。通過建模,可以將複雜的數學問題簡化成形象直觀的計算方式,讓孩子更容易地理解。

圖片來源:海峽時報
Concrete-Pictorial-Abstract(具體、圖像、抽象)是一個重要的教學過程。小朋友會從具體情境開始學習,再以圖像學習,最後才學習抽象概念。例如:
Concrete(具象化)
具象化主要就是使用數學教具,這塊主要用來培養孩子的數感。
朋友面前放著8朵花,老師就放著12朵花,那麼老師比小朋友多幾多朵花呢?(這是拿真實的道具讓孩子學習);
Pictorial(形象化)
形象化,是通過圖像符號,將問題表述出來,是為由形象向抽象過渡做準備。
老師會請小朋友畫出8朵花,再為老師畫出12朵花,請問老師比小朋友多幾多朵花呢?
Abstract(抽象化)
抽象化就是具體的建模了。建模將複雜的數學問題抽象為簡單的數學圖形,方便孩子理解。

圖片來源:海峽時報
根據學習理論,年紀小的學生更適合利用圖式學習,因為這能讓他們更好地想像問題的結構,並理解問題中不同數目之間的關係。符號的使用和操作更為抽象,因此更適合年齡較大的學生,如中學生。
當然了考試中任何用於解答考題的方法都是被接受的,只要提出的解決方案在數學上是合理、清晰和符合邏輯,這也包括代數方法(algebra),只不過在考試出題方面使用代數方法更加複雜。
家長需要注意的地方
堅持使用,因為它是培養孩子的一種思維模式,需要不斷練習讓孩子形成習慣,能條件反射地去使用,達到「不知道"自己知道的狀態。
該方法要讓孩子甚至能在沒有紙筆的時候,看到一道題目腦海里也能浮想出清晰的圖形關係,這樣遇到複雜一點兒的數學題目才能保持思路清晰,有條不紊。
孩子畫圖的時候注意引導他儘量按照數量的比例來畫,這樣更直觀,也更容易提早「猜"出答案,這點有些類似我們以前做幾何題,圖畫得好畫得準確的話對解題很有幫助。
建模方法可以在孩子平時做任何數學作業題時使用,不一定非得用新加坡的教材或練習冊,當然它能讓家長省點勁兒。
父母不是老師,不應該指望教他們的孩子解決學業問題。家長不要在孩子面前一直強調自己的數學很弱,因為這可能會影響孩子,讓他低估自己的潛力。
父母可以表達對數學及其所學內容的興趣,從而激發他們的興趣並為終身學習樹立榜樣。還可以鼓勵孩子定期練習和複習數學,而不要死記硬背。