在中国,家长们对于孩子的数学教育选择常常陷入纠结。
新加坡数学、美国数学和中国数学,这三大派系各有其追随者和粉丝。
"
每当提及新加坡数学,家长们总会提到其严谨的教学体系和突出的国际成就;
而谈到美国数学,大家又会强调其创新性和实用性;
当然,也有许多家长坚信,最传统的中国数学教育才是最适合孩子的。
"

然而,这些数学体系究竟有何独特之处?
它们之间又有何差异?
为什么新加坡数学能够赢得全球60多个国家和地区的青睐,被广泛用于教育强国如美国、英国、法国等?
为了解答这些问题,我们深入研究了这三大数学派系,并为您带来了全面的测评和解析。
新加坡 VS. 美国数学 VS. 中国数学
01 教材难度
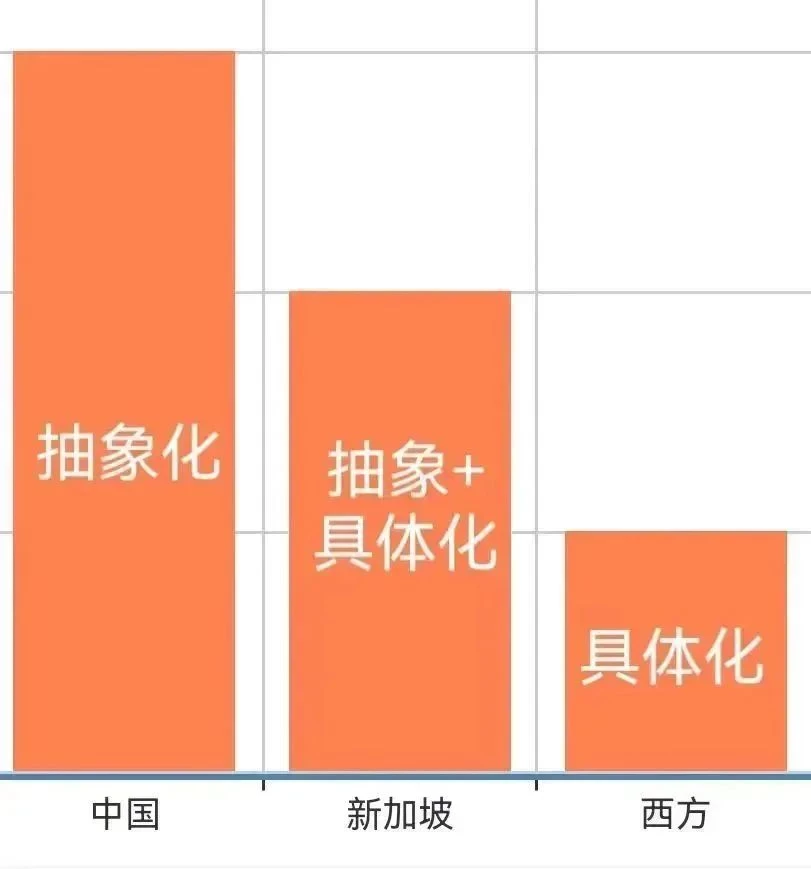
新加坡教材
抽象+具体化(难度适中)
美国教材
具体化(难度简单)
中国教材
抽象化(难度较大)
按照难度从高到低的排序,中国数学位列首位,其次是新加坡数学,而美国数学则位居第三。
这一结果与大众对于中国数学难度固有的认知相符,证明了其在数学教育领域的难度相对较高。
02 教材实用性
新加坡数学教材的另一个显著特点是其与实际生活的紧密结合。
通过采用孩子们日常生活中能接触到的场景,如年龄、交通、食物和购物等作为例子,使得数学概念更加贴近生活,更容易引发联想,帮助孩子们快速理解。
其次是美国,最后才是中国,咱们都知道中国的课本比较偏向于鲜明的公式和算法,学生一般要在教师的讲解下才能理解公式的含义,甚至也有的学生会死记硬背。
03 思维训练
咱们以一道算术题来举例:
桌上放着三个橙子和两个苹果,那么桌上一共有几个水果?
那么中国的老师可能会让孩子先背诵十以内的加减法,让孩子从公式中更快更直接地地得出答案。
而美国的老师会拿出三个橙子和两个苹果,让孩子亲身体验,去数一数有几个水果。
这样的教学方法让孩子容易接受,但同时也耗费时间和精力,会拖慢学生的学习进度。
而新加坡的老师会将“橙子”“苹果”正在具象化的东西转化成图形,让孩子从中学会算数。
具体和抽象化相结合的教学节省了教学时间,加快了教学节奏,也让孩子更易接受。
教学目标
01 美国
数学
美国数学注重对数学概念的理解和构建,强调在实践探索中培养孩子的思考能力。
在解题过程中,美国数学倾向于将抽象化的过程以实际现象的形式来呈现,但有时这反而会使原本简单的问题变得更加复杂。
例如,对于某道题,美国的解法可能会首先画出苹果与橙子的图形,然后寻找具有相同形状的模具,强调这两者都是水果,因此可以直接相加。
02 中国数学
相比之下,中国数学更注重应用解题。
通过大量的题目训练,提高数学解题的效率和准确率。
在教学过程中,中国数学侧重于训练学生的头脑计算能力和记忆能力,例如教授运算口诀和背诵运算公式等。
在解答应用题时,中国学生五年级就开始学习使用代数符号,如x、y等,来书写公式和解决问题。
例如,对于某道题,中国数学可能会直接列出橙子和苹果的数量,并要求学生直接计算。
03
新加坡数学
新加坡数学则结合了中国数学的具象化和美国数学的抽象化特点。
它侧重于使用图像建模(即CPA教学法),要求学生通过绘制模型的方式将抽象概念具体化。
新加坡数学强调培养学生的建立数学模型的能力,帮助他们更清晰地掌握解题思路,内化数学思维。
例如,对于上述的例题,新加坡数学可能会将苹果和橙子都建模为方形块,使学生明白两者都代表水果,因此可以直接相加。
综上所述,新加坡数学显然融合了中美国的优点。
在难度上,它与中国数学相接轨,而在学习方式和理念上则更接近美国数学。
这避免了中国的“填鸭式”教育方式,弥补了中国传统数学在思维拓展方面的不足。
因此,无论从教材难度、实用性,还是思维训练以及各类数学竞赛考试的角度来看,新加坡数学无疑是更合适的选择。
新加坡数学的精华在哪里?
新加坡数学的核心教学方法是CPA教学法,这种教学法通过长期的训练,可以帮助孩子建立全面而系统的数学思维,并使他们能够找到数学与生活中的实际联系,从而在面对复杂的数学问题时,能够快速理清解题思路并找到有效的解决办法。
01 具象化(C)
是这种教学方法的第一个阶段,它主要是通过使用数学教具,将数学问题转化为日常生活中的实际问题,这样可以帮助孩子更好地理解和应用数学,培养他们的数感。
02 形象化(P)
是第二个阶段,它通过图像将问题表述出来,为向抽象化过渡做准备。这个阶段将数学问题以图像的形式展示出来,使孩子能够更直观地理解问题,为后续的抽象化阶段打下基础。
03 抽象化(A)
是最后一个阶段,它具体涉及到建模。
在这个阶段,复杂的数学问题被抽象为简单的数学图形,这样更方便孩子理解并解决问题。
这种教学方法不仅提高了孩子的解题能力,也培养了他们的数学思维和创新能力。
建模方法对培养孩子的数学思维具有显著益处,主要体现在以下三个方面:
01
首先,通过建模的方式给孩子讲解数学题目,可以使问题变得直观而具体,有助于孩子理解。
02
同时,当孩子尝试使用建模方法解决数学问题时,家长可以从他们绘制的图形中观察他们对知识点的掌握情况,从而判断他们是否完全理解和掌握相关内容,是否存在理解盲区。
03
其次,建模方法可以使孩子不惧怕难题,并乐于接受挑战。因为孩子了解到,如果遇到一下子无法解决的问题,可以通过建模方法逐步分解问题,使思路逐渐清晰。
在这个过程中,孩子会获得强烈的成就感,并逐渐建立起解决问题的信心。
例如:
题目一:3+2=5
第一步:(先用具象的小球表示)
第二步:把球去掉,用方块代替
第三步:去掉方框,抽象化
从而让孩子一步一步在脑中形成抽象化的数字加减法观念,逐步熟练运用加减法。
许多孩子觉得数学困难,往往是因为他们没有顺利地从具象的数学概念过渡到抽象的数学概念。
在数学启蒙阶段,孩子们可以通过掰手指、数积木等方式来接触数学,这些方式是具体、有趣且与日常生活密切相关的。
然而,当他们开始接触到抽象的数字符号和运算公式时,数学变得更加不可见和抽象。
对于不适应这种转变的孩子来说,他们很容易因此而产生对数学的畏难心理。

建模可以帮助孩子将数学可视化、直观化,将抽象的数学概念转化为可见的、可触摸的,以及便于与其他人讨论交流的东西。
建模可以被视为连接数学具象与抽象之间的桥梁,它帮助孩子们更好地理解和掌握数学概念。