在中國,家長們對於孩子的數學教育選擇常常陷入糾結。
新加坡數學、美國數學和中國數學,這三大派系各有其追隨者和粉絲。
"
每當提及新加坡數學,家長們總會提到其嚴謹的教學體系和突出的國際成就;
而談到美國數學,大家又會強調其創新性和實用性;
當然,也有許多家長堅信,最傳統的中國數學教育才是最適合孩子的。
"

然而,這些數學體系究竟有何獨特之處?
它們之間又有何差異?
為什麼新加坡數學能夠贏得全球60多個國家和地區的青睞,被廣泛用於教育強國如美國、英國、法國等?
為了解答這些問題,我們深入研究了這三大數學派系,並為您帶來了全面的測評和解析。
新加坡 VS. 美國數學 VS. 中國數學
01 教材難度
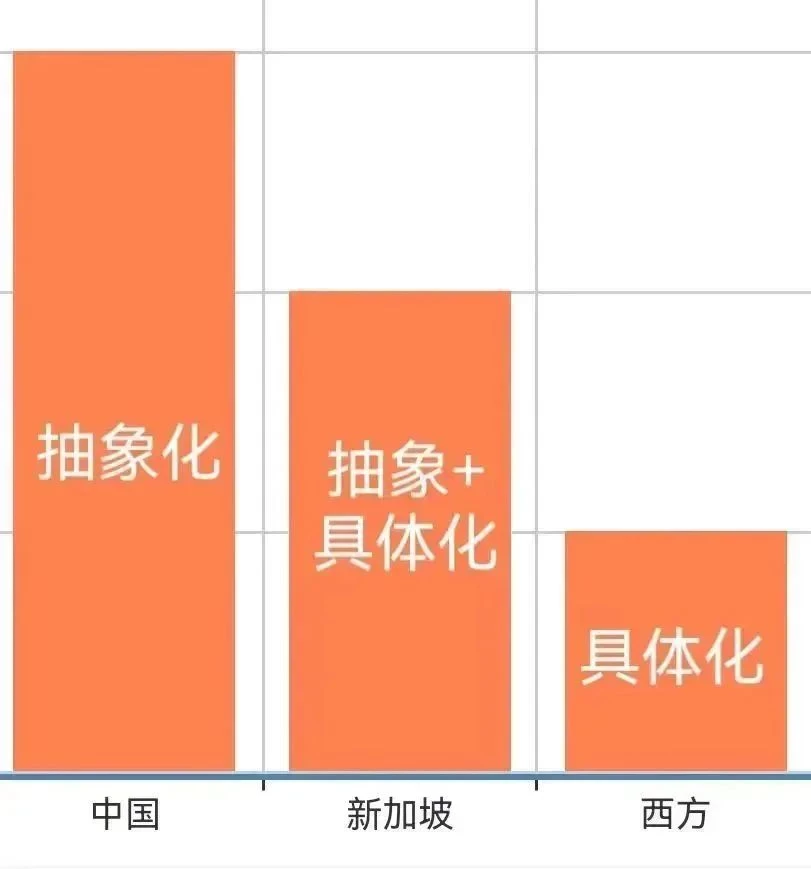
新加坡教材
抽象+具體化(難度適中)
美國教材
具體化(難度簡單)
中國教材
抽象化(難度較大)
按照難度從高到低的排序,中國數學位列首位,其次是新加坡數學,而美國數學則位居第三。
這一結果與大眾對於中國數學難度固有的認知相符,證明了其在數學教育領域的難度相對較高。
02 教材實用性
新加坡數學教材的另一個顯著特點是其與實際生活的緊密結合。
通過採用孩子們日常生活中能接觸到的場景,如年齡、交通、食物和購物等作為例子,使得數學概念更加貼近生活,更容易引發聯想,幫助孩子們快速理解。
其次是美國,最後才是中國,咱們都知道中國的課本比較偏向於鮮明的公式和算法,學生一般要在教師的講解下才能理解公式的含義,甚至也有的學生會死記硬背。
03 思維訓練
咱們以一道算術題來舉例:
桌上放著三個橙子和兩個蘋果,那麼桌上一共有幾個水果?
那麼中國的老師可能會讓孩子先背誦十以內的加減法,讓孩子從公式中更快更直接地地得出答案。
而美國的老師會拿出三個橙子和兩個蘋果,讓孩子親身體驗,去數一數有幾個水果。
這樣的教學方法讓孩子容易接受,但同時也耗費時間和精力,會拖慢學生的學習進度。
而新加坡的老師會將「橙子」「蘋果」正在具象化的東西轉化成圖形,讓孩子從中學會算數。
具體和抽象化相結合的教學節省了教學時間,加快了教學節奏,也讓孩子更易接受。
教學目標
01 美國
數學
美國數學注重對數學概念的理解和構建,強調在實踐探索中培養孩子的思考能力。
在解題過程中,美國數學傾向於將抽象化的過程以實際現象的形式來呈現,但有時這反而會使原本簡單的問題變得更加複雜。
例如,對於某道題,美國的解法可能會首先畫出蘋果與橙子的圖形,然後尋找具有相同形狀的模具,強調這兩者都是水果,因此可以直接相加。
02 中國數學
相比之下,中國數學更注重應用解題。
通過大量的題目訓練,提高數學解題的效率和準確率。
在教學過程中,中國數學側重於訓練學生的頭腦計算能力和記憶能力,例如教授運算口訣和背誦運算公式等。
在解答應用題時,中國學生五年級就開始學習使用代數符號,如x、y等,來書寫公式和解決問題。
例如,對於某道題,中國數學可能會直接列出橙子和蘋果的數量,並要求學生直接計算。
03
新加坡數學
新加坡數學則結合了中國數學的具象化和美國數學的抽象化特點。
它側重於使用圖像建模(即CPA教學法),要求學生通過繪製模型的方式將抽象概念具體化。
新加坡數學強調培養學生的建立數學模型的能力,幫助他們更清晰地掌握解題思路,內化數學思維。
例如,對於上述的例題,新加坡數學可能會將蘋果和橙子都建模為方形塊,使學生明白兩者都代表水果,因此可以直接相加。
綜上所述,新加坡數學顯然融合了中美國的優點。
在難度上,它與中國數學相接軌,而在學習方式和理念上則更接近美國數學。
這避免了中國的「填鴨式」教育方式,彌補了中國傳統數學在思維拓展方面的不足。
因此,無論從教材難度、實用性,還是思維訓練以及各類數學競賽考試的角度來看,新加坡數學無疑是更合適的選擇。
新加坡數學的精華在哪裡?
新加坡數學的核心教學方法是CPA教學法,這種教學法通過長期的訓練,可以幫助孩子建立全面而系統的數學思維,並使他們能夠找到數學與生活中的實際聯繫,從而在面對複雜的數學問題時,能夠快速理清解題思路並找到有效的解決辦法。
01 具象化(C)
是這種教學方法的第一個階段,它主要是通過使用數學教具,將數學問題轉化為日常生活中的實際問題,這樣可以幫助孩子更好地理解和應用數學,培養他們的數感。
02 形象化(P)
是第二個階段,它通過圖像將問題表述出來,為向抽象化過渡做準備。這個階段將數學問題以圖像的形式展示出來,使孩子能夠更直觀地理解問題,為後續的抽象化階段打下基礎。
03 抽象化(A)
是最後一個階段,它具體涉及到建模。
在這個階段,複雜的數學問題被抽象為簡單的數學圖形,這樣更方便孩子理解並解決問題。
這種教學方法不僅提高了孩子的解題能力,也培養了他們的數學思維和創新能力。
建模方法對培養孩子的數學思維具有顯著益處,主要體現在以下三個方面:
01
首先,通過建模的方式給孩子講解數學題目,可以使問題變得直觀而具體,有助於孩子理解。
02
同時,當孩子嘗試使用建模方法解決數學問題時,家長可以從他們繪製的圖形中觀察他們對知識點的掌握情況,從而判斷他們是否完全理解和掌握相關內容,是否存在理解盲區。
03
其次,建模方法可以使孩子不懼怕難題,並樂於接受挑戰。因為孩子了解到,如果遇到一下子無法解決的問題,可以通過建模方法逐步分解問題,使思路逐漸清晰。
在這個過程中,孩子會獲得強烈的成就感,並逐漸建立起解決問題的信心。
例如:
題目一:3+2=5
第一步:(先用具象的小球表示)
第二步:把球去掉,用方塊代替
第三步:去掉方框,抽象化
從而讓孩子一步一步在腦中形成抽象化的數字加減法觀念,逐步熟練運用加減法。
許多孩子覺得數學困難,往往是因為他們沒有順利地從具象的數學概念過渡到抽象的數學概念。
在數學啟蒙階段,孩子們可以通過掰手指、數積木等方式來接觸數學,這些方式是具體、有趣且與日常生活密切相關的。
然而,當他們開始接觸到抽象的數字符號和運算公式時,數學變得更加不可見和抽象。
對於不適應這種轉變的孩子來說,他們很容易因此而產生對數學的畏難心理。

建模可以幫助孩子將數學可視化、直觀化,將抽象的數學概念轉化為可見的、可觸摸的,以及便於與其他人討論交流的東西。
建模可以被視為連接數學具象與抽象之間的橋樑,它幫助孩子們更好地理解和掌握數學概念。
























